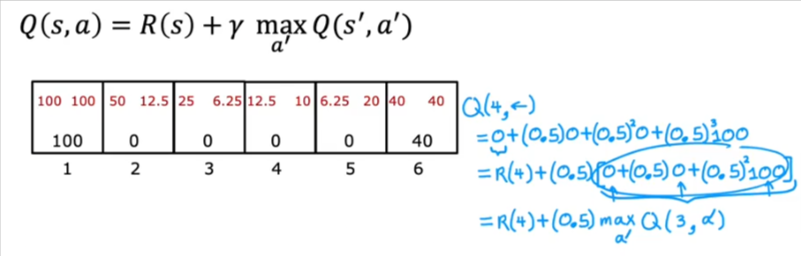Reinforcement Learning

If we are trying to control a robot, or an autonomus helicopter, supervised learning doesn’t work. Reinforcement learning is the way to do it.

We have to tell it what to do it rather than how to do it and we use the reward function to display our response. like training a puppy.

Rover Over Mars

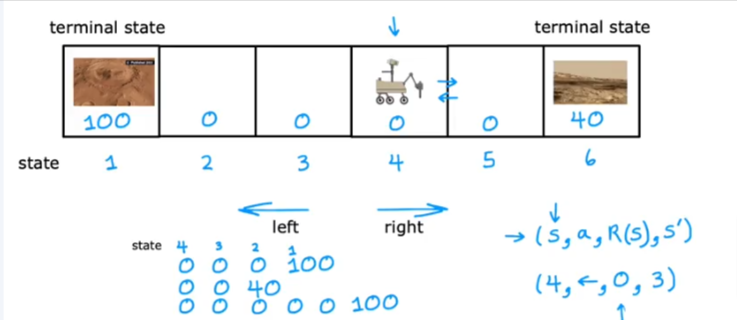
  • If we assign a reward value to each box so how to we get the rover to get to state 1
  • The terminal state are 1 and 6 that’s where the road ends for now
  • It could go left, left…. or it can go right, left, left, right… in any combination
  • s = state
  • a = action (left or right)
  • R = reward
  • s’ is the state associated with the reward given

Return

  • So we have to evaluate the reward for our steps
  • Discount factor if we set to 0.9 is multiplied to each step
  • So the discount decreases the true value of the reward as we keep moving

  • Let’s say we will always go to the left and if we start in each of the states the return is calculated and placed in the boxes below
  • If we reverse the movement the rewards are shown again

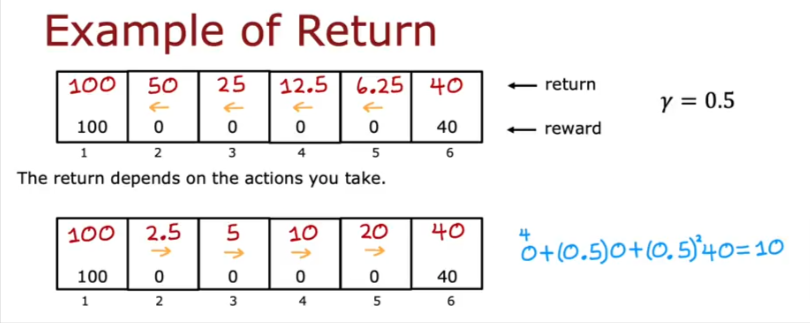
  • If we mix our movement to both L and R we get the following rewards for each state/box
  • So if we start in box 5 and go to the right we end up with 20

Policy

  • We can always go to the nearest reward
  • Go to larger reward
  • Always go left….
  • We can have a policy that takes a state s, maps a policy \(\pi\) to it and we get the reward.

MDP

Markov Decision Process - The future only depends on the current state not how you got here.

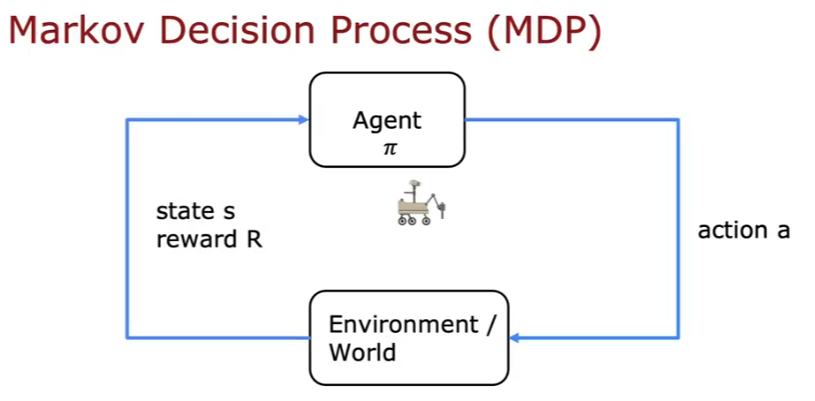
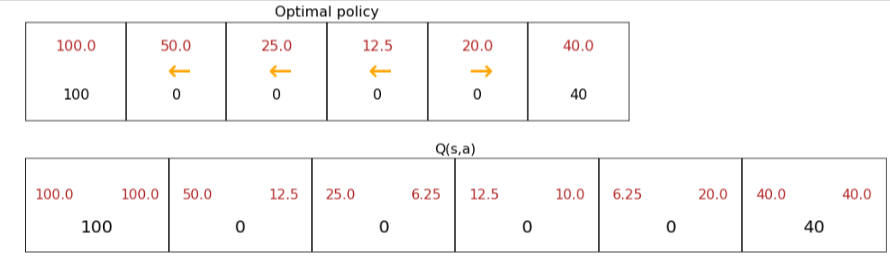
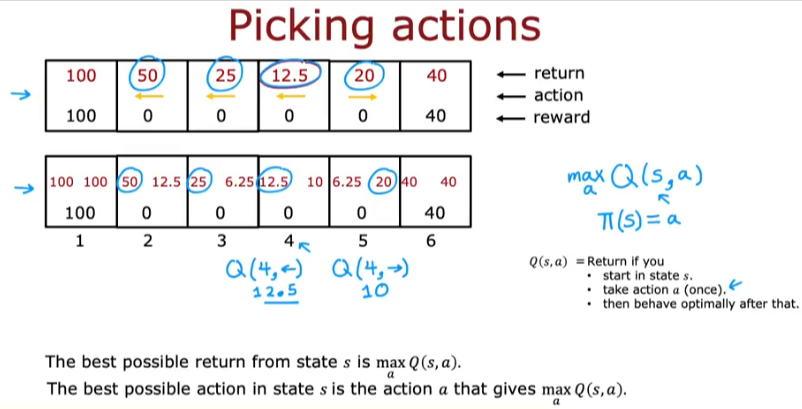
State Action Value

  • Take action a and follow the optimal policy after that
  • So if we have the good policy to be to go left from state 4 and go right from state 5 (if we think that’s the optimal policy/solution)

  • So if we clean up the image above we get to see what the best move would be in each state as shown in each box with the left and right numbers
  • For example if you look at state 4, going left gives us a return of 12.5
  • and going right gives us 10
  • So if we are at state 4 the optimal move would be left
  • So when you have Q() for each state, then when you arrive to every state you will have one optimal move

Bellman Equation

How do we compute the Q(s,a) values? We use the Bellman Equation.

  • Remember R(s) is the reward in that state
  • Let’s set factor \(\gamma\) = 0.5

Example

  • Note in the terminal state we get R(s) = Immediate reward
  • The second part of the equation is the return for behaving optimally starting from state s’

import numpy as np
from utils import *

num_states = 6
num_actions = 2

terminal_left_reward = 100
terminal_right_reward = 40
each_step_reward = 0

# Discount factor
gamma = 0.5

# Probability of going in the wrong direction
misstep_prob = 0

generate_visualization(terminal_left_reward, terminal_right_reward, each_step_reward, gamma, misstep_prob)