Discrete vs Continuous
The position of the helicopter has more than just discrete stages. It can move in many different direction, with different velocity, angle, pitch, yaw, row, height above ground… and how fast each parameter is changing, so the continuous state is represented with a vector
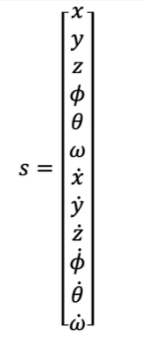
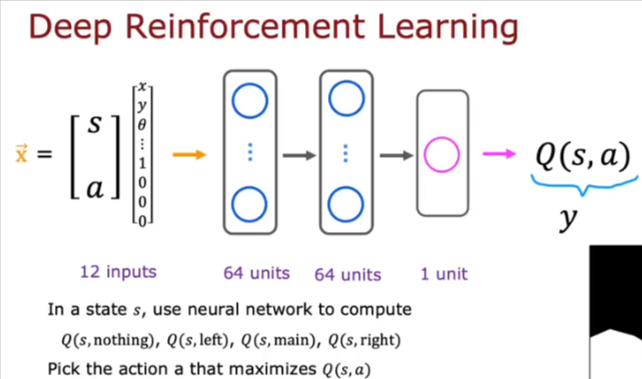
State-Value Function
We want to create a NN that inputs the current state and outputs an estimate of Q(s,a).
- Action could be any of 4 actions indicated by 0 or 1 for the corresponding action
- So nothing would be 1,0,0,0 and Left= 0,1,0,0 …
So how do we train a NN to output Q(s,a)? we use a large dataset for x and y and then use supervised learning like we have done before.
How do we get the training values x and y? Let’s look at the Bellman Equation from the last page
- So we take different actions randomly from random states and observe the actions and rewards
- So we get a bunch of tuples from which the first two give us x values and the second two give us y values
- We also take a guess at the Q() function

Learning Algorithm
So let’s put it together:
- Guess a random value for Q()
- Take random actions from random states
- Store the most recent 10000 tuples
- To train the NN:
- create training set of 10000 examples using the formulas shown below

Refine Algorithm
So as we keep running the algorithm Q hopefully becomes a better estimation, so we keep running it till? We can make a refinement to improve our process:
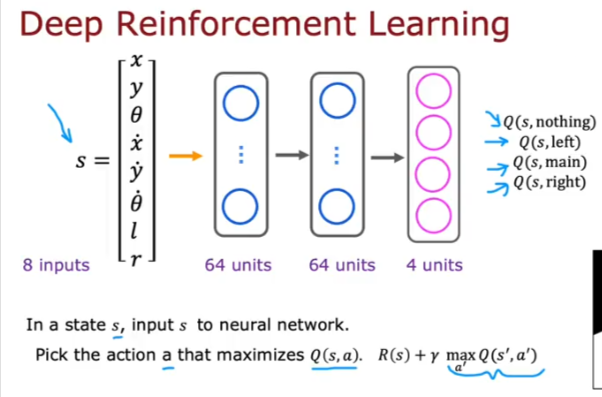
- We can pick a network that will estimate all 4 output units together instead of one at a time as we did above
Greedy Policy
While we are training our NN we don’t know the best action till we are done learning. But what if we try to optimize the way we randomly choose the action to take?
- Pick the action randomly instead of trying to maximize the Q value, because if it knows that firing the main thruster is a bad idea it will never try it. But we want it to try all actions and see what happens.
- So to make it take exploratory actions use the lower probability and choose randomly
- If you start high estimation and gradually decrease is another example

- This type of algorithm takes more time to train efficiently if the parameters are chosen wildly