Making Recommendations
Recommender is what you experience when sites make recommendations whether a movie, a product….
Movie Recommendations
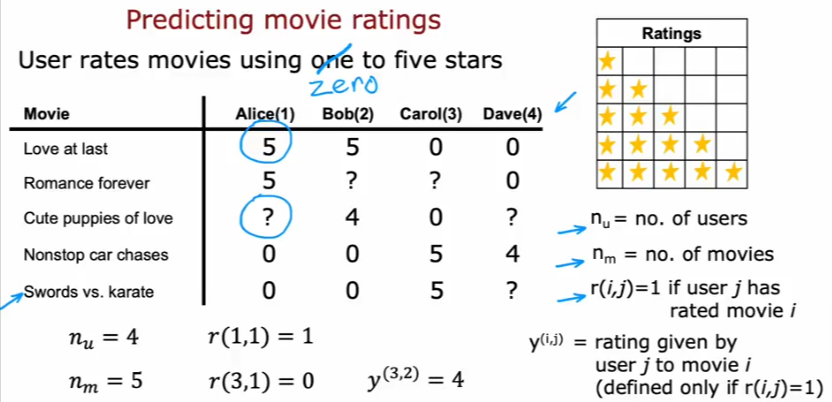
Let’s say we have a small dataset of movie reviews:
- nu = no of users
- nm = no of movies
- r(i,j) =1 if user j has rated movie i
- y(i,j) = rating given by user j to movie i which is defined only if r(i,j)=1
- Note not every user has rated all the movies
Let’s predict how users will rate the movies that have not been rated
Before we proceed let’s raise another possibility:
- What if we have more features regarding these movies such as (x1=romance & x2=action) would that help predict what the users will rate the movies
- What if we don’t have any additional features?
We’ll cover the first option first:
Added Features
- The values of whether it is that features vary from 0 -1 with 0 being least or not and 1 being definitely
- Here is an example, if a movie has x1=0.9 it means it is highly romantic and if x2=0.1 means it is not an action movie
- Let n=number of features
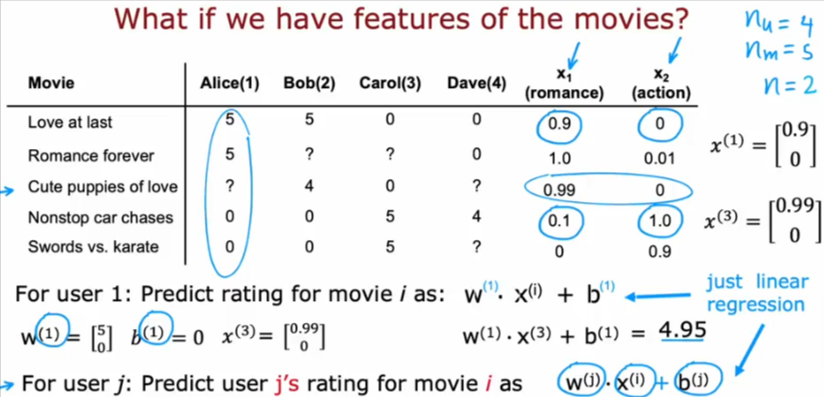
Let’s predict the rating of Cute puppies of love for Alice
- we will use the linear regression algorithm W * X(i) + b
- Let’s pretend the value of w= [5, 0] and b =0 and from the table X(3)=[0.99, 0]
- Note since we have two features X that’s why we needed two values for W
- So the algorithm will give us 4.95
- Which seems reasonable since she rated the two other romantic movies high as well
- The superscript of 1 stands for the fact that Alice if the first user in the dataset, and so each user will have their own 1-4 since we have 4 users
- So the generalized algorithm to predict the rating for any user will have the (j) superscript as shown in the image
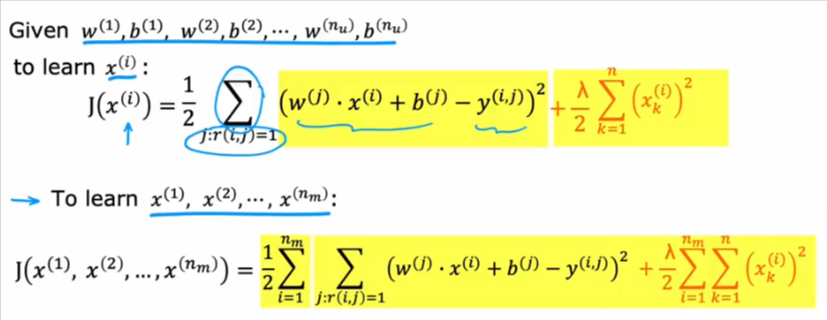
Cost Function
- As you see below it will be the value predicted - the actual value rated
- But since there are some cases when users have not rated all the movies so how can we sum over all the data rows, well we won’t
- This is it differs from linear regression because we only sum over the RATED movies
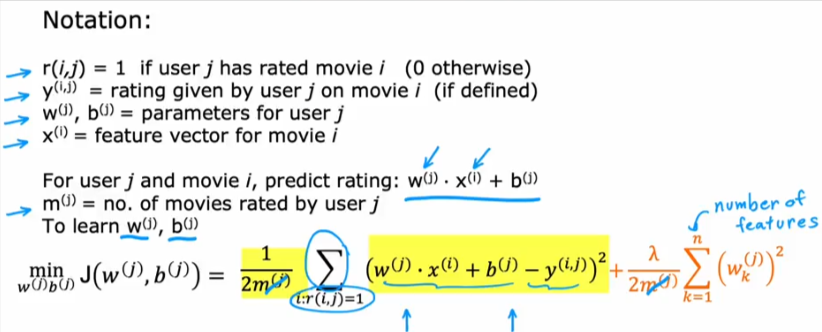
- To learn the parameters we need to minimize the cost function

Blank Features

What if we haven’t learned the values of the added features? Let’s say a movie just came out and for some reason nobody has rated the added features.
- Can we predict what each user will rate the added features
- Let’s pretend we know the values of w and b for each user as shown in the image
- As you see all the values of b are 0 so let’s ignore b from the formula
- So if you have all the ratings from all users for a certain movie you can predict x1
- Then you can predict x2
- And now that you have both x values you can try to predict the ratings that are missing for all the users to all movies as shown above
- If you don’t have all ratings to a movie from all users you cannot predict x values
Cost Function
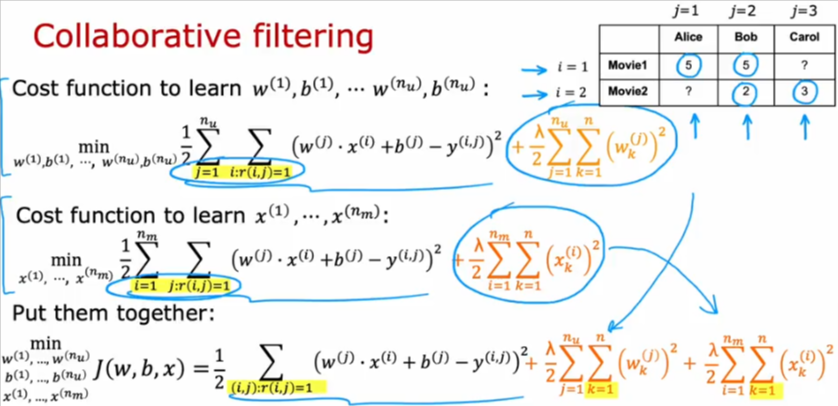
Collaborative Filtering
Let’s put both scenarios detailed above together.
Gradient Descent
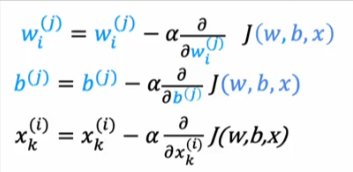
Binary Labels
Sometimes we just ask the user if they like something or not, this is a simple binary model. So we can revert back to what we’ve already learned to learn if we should recommend an item or not.
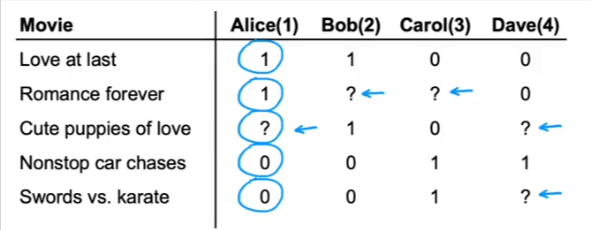
- Some users have not commented on the item
- Here is the breakdown

- Now that we are using binary values we just need to predict the probability which is a binary classification model
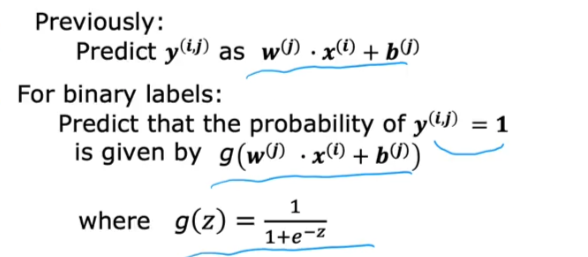
Cost Function
Now the cost function for binary classification will become:

Mean Normalization
It will make the algorithm make better prediction and speed it up if we normalize the reviews by the users

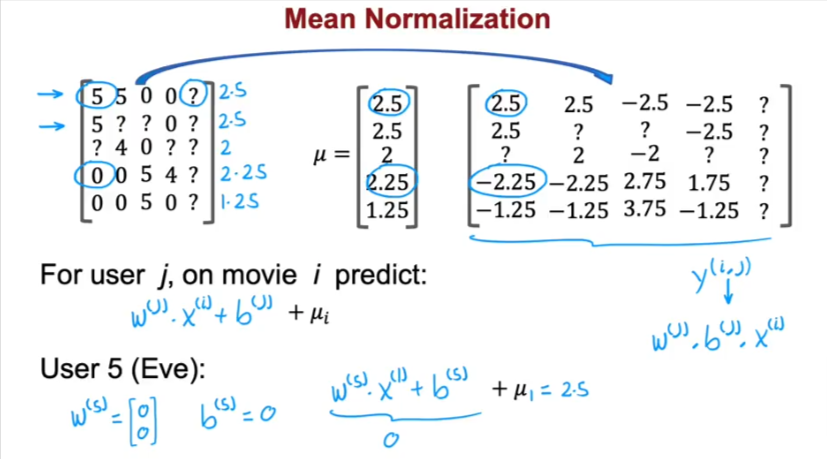
- So let’s take all the data/reviews and put them in a 2D matrix
- We take all the rows and average them out, if we have a movie that hasn’t been shown to anyone we can average out the columns instead
- Of course we skip the ? marks
- Now we get a vector of average ratings
- Then we take the original ratings and subtract the mean/average values from it and now we have a new matrix
- Then to predict the new rating we use the same formula as we did above but in order to not have a negative rating (since the rating system is from 0-5) we must add back the mean/average value for each row/movie which is \(\mu\) i
- So user 5 will have a rating of 2.5 for the first movie i=1
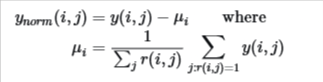
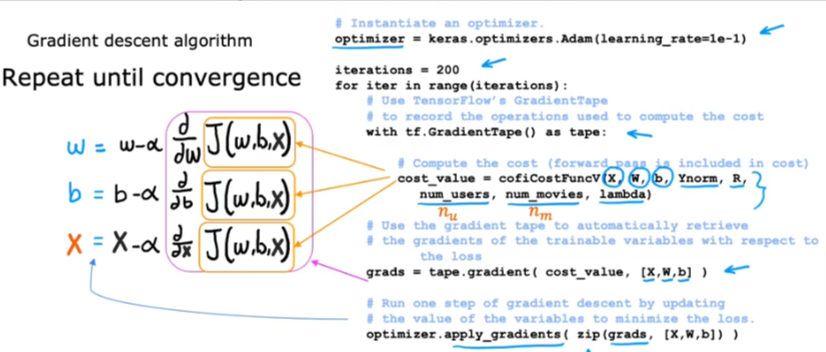
TF Implementation
- First we specify the optimizer: Adam in this case
- Choose number of iterations
- Loop through the number of iterations we call the GradientTape which will record the values
- In the loop you will see the cost function J which takes inputs: X, W, B, Ynorm are the normalized mean. Which values have a rating, number of users, number of movies, as well as the regularization parameter \(\lambda\)
- This cost_value will figure out the derivatives
- Then we feed the derivatives into the gradient to give us the gradient
- We run it, and repeat it by updating the values of the variables to minimize the loss using the optimizer we specified