Hyperparameters

Lunar Landing

We will be using OpenAI’s Gym Library. The Gym library provides a wide variety of environments for reinforcement learning. To put it simply, an environment represents a problem or task to be solved. We will try to solve the Lunar Lander environment using reinforcement learning.

  • The goal of the Lunar Lander environment is to land the lunar lander safely on the landing pad on the surface of the moon.
  • The landing pad is designated by two flag poles and its center is at coordinates (0,0) but the lander is also allowed to land outside of the landing pad.
  • The lander starts at the top center of the environment with a random initial force applied to its center of mass and has infinite fuel.
  • The environment is considered solved if you get 200 points.

Action Space

The agent has four discrete actions available:

  • Do nothing.
  • Fire right engine.
  • Fire main engine.
  • Fire left engine.

Each action has a corresponding numerical value:

Do nothing = 0 Fire right engine = 1 Fire main engine = 2 Fire left engine = 3

Observation Space

The agent’s observation space consists of a state vector with 8 variables:

  • Its (π‘₯,𝑦)(x,y) coordinates. The landing pad is always at coordinates (0,0)(0,0).
  • Its linear velocities (π‘₯Λ™,𝑦˙)(xΛ™,yΛ™).
  • Its angle πœƒΞΈ.
  • Its angular velocity πœƒΛ™ΞΈΛ™.
  • Two booleans, 𝑙l and π‘Ÿr, that represent whether each leg is in contact with the ground or not.

Rewards

After every step, a reward is granted. The total reward of an episode is the sum of the rewards for all the steps within that episode.

For each step, the reward:

  • is increased/decreased the closer/further the lander is to the landing pad.
  • is increased/decreased the slower/faster the lander is moving.
  • is decreased the more the lander is tilted (angle not horizontal).
  • is increased by 10 points for each leg that is in contact with the ground.
  • is decreased by 0.03 points each frame a side engine is firing.
  • is decreased by 0.3 points each frame the main engine is firing.

The episode receives an additional reward of -100 or +100 points for crashing or landing safely respectively.

Episode Termination

An episode ends (i.e the environment enters a terminal state) if:

  • The lunar lander crashes (i.e if the body of the lunar lander comes in contact with the surface of the moon).
  • The absolute value of the lander’s π‘₯x-coordinate is greater than 1 (i.e. it goes beyond the left or right border)

You can check out the Open AI Gym documentation for a full description of the environment.

Setup

import time
from collections import deque, namedtuple

import gym
import numpy as np
import PIL.Image
import tensorflow as tf
import utils

from pyvirtualdisplay import Display
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense, Input
from tensorflow.keras.losses import MSE
from tensorflow.keras.optimizers import Adam
# Set up a virtual display to render the Lunar Lander environment.
Display(visible=0, size=(840, 480)).start();

# Set the random seed for TensorFlow
tf.random.set_seed(utils.SEED)
MEMORY_SIZE = 100_000     # size of memory buffer
GAMMA = 0.995             # discount factor
ALPHA = 1e-3              # learning rate  
NUM_STEPS_FOR_UPDATE = 4  # perform a learning update every C time steps

Load Environment

We start by loading the LunarLander-v2 environment from the gym library by using the .make() method. LunarLander-v2 is the latest version of the Lunar Lander environment and you can read about its version history in the Open AI Gym documentation.

env = gym.make('LunarLander-v2')

Reset to Orig State

Once we load the environment we use the .reset() method to reset the environment to the initial state. The lander starts at the top center of the environment and we can render the first frame of the environment by using the .render() method.

env.reset()
PIL.Image.fromarray(env.render(mode='rgb_array'))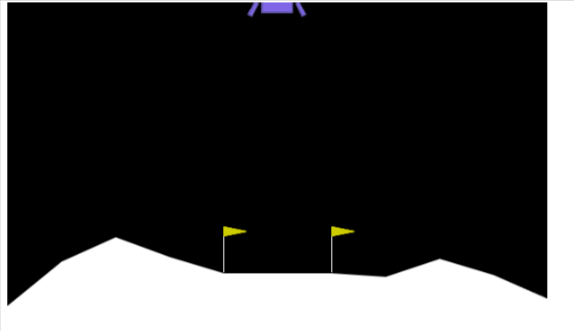

Get the size of the state vector and the number of valid actions.

state_size = env.observation_space.shape
num_actions = env.action_space.n

print('State Shape:', state_size)
print('Number of actions:', num_actions)
State Shape: (8,) Number of actions: 4

Interact with Environment

In the standard β€œagent-environment loop” formalism, an agent interacts with the environment in discrete time steps 𝑑=0,1,2,…t=0,1,2,…. At each time step 𝑑t, the agent uses a policy πœ‹Ο€ to select an action 𝐴𝑑At based on its observation of the environment’s state 𝑆𝑑St. The agent receives a numerical reward 𝑅𝑑Rt and on the next time step, moves to a new state 𝑆𝑑+1St+1.

Exploring the Environment’s Dynamics

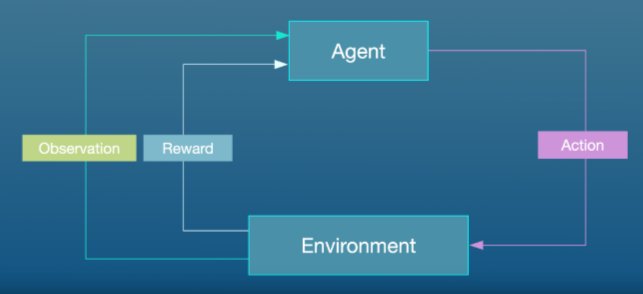
In Open AI’s Gym environments, we use the .step() method to run a single time step of the environment’s dynamics. In the version of gym that we are using the .step() method accepts an action and returns four values:

  • observation (object): an environment-specific object representing your observation of the environment. In the Lunar Lander environment this corresponds to a numpy array containing the positions and velocities of the lander as described in section 3.2 Observation Space.
  • reward (float): amount of reward returned as a result of taking the given action. In the Lunar Lander environment this corresponds to a float of type numpy.float64 as described in section 3.3 Rewards.
  • done (boolean): When done is True, it indicates the episode has terminated and it’s time to reset the environment.
  • info (dictionary): diagnostic information useful for debugging. We won’t be using this variable in this notebook but it is shown here for completeness.

To begin an episode, we need to reset the environment to an initial state. We do this by using the .reset() method.

# Reset the environment and get the initial state.
current_state = env.reset()

Once the environment is reset, the agent can start taking actions in the environment by using the .step() method. Note that the agent can only take one action per time step.

In the cell below you can select different actions and see how the returned values change depending on the action taken. Remember that in this environment the agent has four discrete actions available and we specify them in code by using their corresponding numerical value:

Do nothing = 0 Fire right engine = 1 Fire main engine = 2 Fire left engine = 3
# Select an action
action = 0

# Run a single time step of the environment's dynamics with the given action.
next_state, reward, done, _ = env.step(action)

# Display table with values.
utils.display_table(current_state, action, next_state, reward, done)

# Replace the `current_state` with the state after the action is taken
current_state = next_state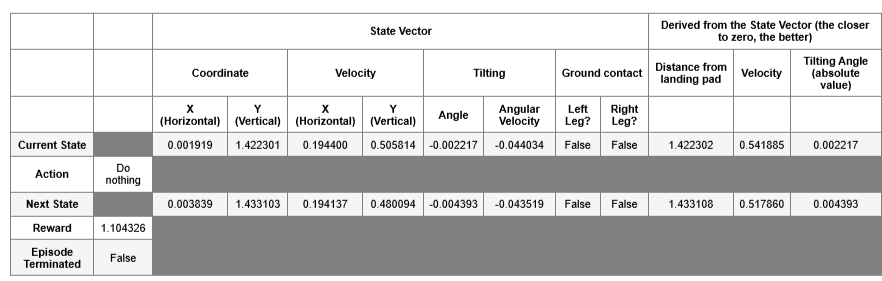

Deep Q - Learning

In cases where both the state and action space are discrete we can estimate the action-value function iteratively by using the Bellman equation:

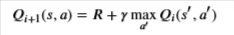
This iterative method converges to the optimal action-value function π‘„βˆ—(𝑠,π‘Ž)Qβˆ—(s,a) as π‘–β†’βˆžiβ†’βˆž. This means that the agent just needs to gradually explore the state-action space and keep updating the estimate of 𝑄(𝑠,π‘Ž)Q(s,a) until it converges to the optimal action-value function π‘„βˆ—(𝑠,π‘Ž)Qβˆ—(s,a). However, in cases where the state space is continuous it becomes practically impossible to explore the entire state-action space. Consequently, this also makes it practically impossible to gradually estimate 𝑄(𝑠,π‘Ž)Q(s,a) until it converges to π‘„βˆ—(𝑠,π‘Ž)Qβˆ—(s,a).

In the Deep 𝑄Q-Learning, we solve this problem by using a neural network to estimate the action-value function 𝑄(𝑠,π‘Ž)β‰ˆπ‘„βˆ—(𝑠,π‘Ž)Q(s,a)β‰ˆQβˆ—(s,a). We call this neural network a 𝑄Q-Network and it can be trained by adjusting its weights at each iteration to minimize the mean-squared error in the Bellman equation.

Unfortunately, using neural networks in reinforcement learning to estimate action-value functions has proven to be highly unstable. Luckily, there’s a couple of techniques that can be employed to avoid instabilities. These techniques consist of using a Target Network and Experience Replay. We will explore these two techniques in the following sections.

Target Network

We can train the 𝑄Q-Network by adjusting it’s weights at each iteration to minimize the mean-squared error in the Bellman equation, where the target values are given by:

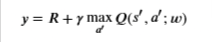
where 𝑀w are the weights of the 𝑄Q-Network. This means that we are adjusting the weights 𝑀w at each iteration to minimize the following error:

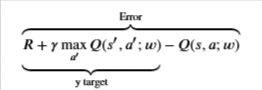
Notice that this forms a problem because the 𝑦y target is changing on every iteration. Having a constantly moving target can lead to oscillations and instabilities. To avoid this, we can create a separate neural network for generating the 𝑦y targets. We call this separate neural network the target 𝑄̂ Q^-Network and it will have the same architecture as the original 𝑄Q-Network. By using the target 𝑄̂ Q^-Network, the above error becomes:

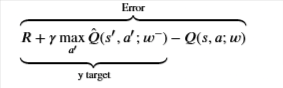
where π‘€βˆ’wβˆ’ and 𝑀w are the weights of the target 𝑄̂ Q^-Network and 𝑄Q-Network, respectively.

In practice, we will use the following algorithm: every 𝐢C time steps we will use the 𝑄̂ Q^-Network to generate the 𝑦y targets and update the weights of the target 𝑄̂ Q^-Network using the weights of the 𝑄Q-Network. We will update the weights π‘€βˆ’wβˆ’ of the the target 𝑄̂ Q^-Network using a soft update. This means that we will update the weights π‘€βˆ’wβˆ’ using the following rule:

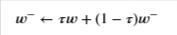
where 𝜏β‰ͺ1Ο„β‰ͺ1. By using the soft update, we are ensuring that the target values, 𝑦y, change slowly, which greatly improves the stability of our learning algorithm.

Create NN

We will create the 𝑄Q and target 𝑄̂ Q^ networks and set the optimizer. Remember that the Deep 𝑄Q-Network (DQN) is a neural network that approximates the action-value function 𝑄(𝑠,π‘Ž)β‰ˆπ‘„βˆ—(𝑠,π‘Ž)Q(s,a)β‰ˆQβˆ—(s,a). It does this by learning how to map states to 𝑄Q values.

To solve the Lunar Lander environment, we are going to employ a DQN with the following architecture:

  • An Input layer that takes state_size as input.
  • A Dense layer with 64 units and a relu activation function.
  • A Dense layer with 64 units and a relu activation function.
  • A Dense layer with num_actions units and a linear activation function. This will be the output layer of our network.

In the cell below you should create the 𝑄Q-Network and the target 𝑄̂ Q^-Network using the model architecture described above. Remember that both the 𝑄Q-Network and the target 𝑄̂ Q^-Network have the same architecture.

Lastly, you should set Adam as the optimizer with a learning rate equal to ALPHA. Recall that ALPHA was defined in the Hyperparameters section. We should note that for this exercise you should use the already imported packages:

# Create the Q-Network
q_network = Sequential([
    Input(shape=state_size),                      
    Dense(units=64, activation='relu'),            
    Dense(units=64, activation='relu'),            
    Dense(units=num_actions, activation='linear'),
    ])

# Create the target Q^-Network
target_q_network = Sequential([
    Input(shape=state_size),                       
    Dense(units=64, activation='relu'),            
    Dense(units=64, activation='relu'),            
    Dense(units=num_actions, activation='linear'), 
    ])

optimizer = Adam(learning_rate=ALPHA)

Experience Replay

When an agent interacts with the environment, the states, actions, and rewards the agent experiences are sequential by nature. If the agent tries to learn from these consecutive experiences it can run into problems due to the strong correlations between them. To avoid this, we employ a technique known as Experience Replay to generate uncorrelated experiences for training our agent. Experience replay consists of storing the agent’s experiences (i.e the states, actions, and rewards the agent receives) in a memory buffer and then sampling a random mini-batch of experiences from the buffer to do the learning. The experience tuples (𝑆𝑑,𝐴𝑑,𝑅𝑑,𝑆𝑑+1)(St,At,Rt,St+1) will be added to the memory buffer at each time step as the agent interacts with the environment.

For convenience, we will store the experiences as named tuples.

By using experience replay we avoid problematic correlations, oscillations and instabilities. In addition, experience replay also allows the agent to potentially use the same experience in multiple weight updates, which increases data efficiency.

# Store experiences as named tuples
experience = namedtuple("Experience", field_names=["state", "action", "reward", "next_state", "done"])

Q-Learning

Now that we know all the techniques that we are going to use, we can put them together to arrive at the Deep Q-Learning Algorithm With Experience Replay.

Loss Function

We  will implement line 12 of the algorithm outlined in Fig 3 above and you will also compute the loss between the 

𝑦y targets and the π‘„(𝑠,π‘Ž)Q(s,a) values. In the cell below, complete the compute_loss function by setting the π‘¦y targets equal to:

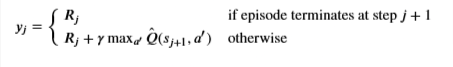
Here are a couple of things to note:

  • The compute_loss function takes in a mini-batch of experience tuples. This mini-batch of experience tuples is unpacked to extract the states, actions, rewards, next_states, and done_vals. You should keep in mind that these variables are TensorFlow Tensors whose size will depend on the mini-batch size. For example, if the mini-batch size is 64 then both rewards and done_vals will be TensorFlow Tensors with 64 elements.
  • Using if/else statements to set the 𝑦y targets will not work when the variables are tensors with many elements. However, notice that you can use the done_vals to implement the above in a single line of code. To do this, recall that the done variable is a Boolean variable that takes the value True when an episode terminates at step 𝑗+1j+1 and it is False otherwise. Taking into account that a Boolean value of True has the numerical value of 1 and a Boolean value of False has the numerical value of 0, you can use the factor (1 - done_vals) to implement the above in a single line of code. Here’s a hint: notice that (1 - done_vals) has a value of 0 when done_vals is True and a value of 1 when done_vals is False.

Lastly, compute the loss by calculating the Mean-Squared Error (MSE) between the y_targets and the q_values. To calculate the mean-squared error you should use the already imported package MSE:

def compute_loss(experiences, gamma, q_network, target_q_network):
    """ 
    Calculates the loss.
    
    Args:
      experiences: (tuple) tuple of ["state", "action", "reward", "next_state", "done"] namedtuples
      gamma: (float) The discount factor.
      q_network: (tf.keras.Sequential) Keras model for predicting the q_values
      target_q_network: (tf.keras.Sequential) Keras model for predicting the targets
          
    Returns:
      loss: (TensorFlow Tensor(shape=(0,), dtype=int32)) the Mean-Squared Error between
            the y targets and the Q(s,a) values.
    """

    # Unpack the mini-batch of experience tuples
    states, actions, rewards, next_states, done_vals = experiences
    
    # Compute max Q^(s,a)
    max_qsa = tf.reduce_max(target_q_network(next_states), axis=-1)
    
    # Set y = R if episode terminates, otherwise set y = R + Ξ³ max Q^(s,a).
    y_targets = rewards + (gamma * max_qsa * (1 - done_vals))
  
    
    # Get the q_values and reshape to match y_targets
    q_values = q_network(states)
    q_values = tf.gather_nd(q_values, tf.stack([tf.range(q_values.shape[0]),
                                                tf.cast(actions, tf.int32)], axis=1))
        
    # Compute the loss
    loss = MSE(y_targets, q_values) 
    
    return loss

Update Network Weights

We will use the agent_learn function below to implement lines 12 -14 of the algorithm outlined in Fig 3. The agent_learn function will update the weights of the 𝑄Q and target 𝑄̂ Q^ networks using a custom training loop. Because we are using a custom training loop we need to retrieve the gradients via a tf.GradientTape instance, and then call optimizer.apply_gradients() to update the weights of our 𝑄Q-Network. Note that we are also using the @tf.function decorator to increase performance. Without this decorator our training will take twice as long. If you would like to know more about how to increase performance with @tf.function take a look at the TensorFlow documentation.

The last line of this function updates the weights of the target 𝑄̂ Q^-Network using a soft update. If you want to know how this is implemented in code we encourage you to take a look at the utils.update_target_network function in the utils module.

@tf.function
def agent_learn(experiences, gamma):
    """
    Updates the weights of the Q networks.
    
    Args:
      experiences: (tuple) tuple of ["state", "action", "reward", "next_state", "done"] namedtuples
      gamma: (float) The discount factor.
    
    """
    
    # Calculate the loss
    with tf.GradientTape() as tape:
        loss = compute_loss(experiences, gamma, q_network, target_q_network)

    # Get the gradients of the loss with respect to the weights.
    gradients = tape.gradient(loss, q_network.trainable_variables)
    
    # Update the weights of the q_network.
    optimizer.apply_gradients(zip(gradients, q_network.trainable_variables))

    # update the weights of target q_network
    utils.update_target_network(q_network, target_q_network)

Train the Agent

We are now ready to train our agent to solve the Lunar Lander environment. In the cell below we will implement the algorithm in Fig 3 line by line (please note that we have included the same algorithm below for easy reference. This will prevent you from scrolling up and down the notebook):

  • Line 1: We initialize the memory_buffer with a capacity of 𝑁=N= MEMORY_SIZE. Notice that we are using a deque as the data structure for our memory_buffer.
  • Line 2: We skip this line since we already initialized the q_network in Exercise 1.
  • Line 3: We initialize the target_q_network by setting its weights to be equal to those of the q_network.
  • Line 4: We start the outer loop. Notice that we have set 𝑀=M= num_episodes = 2000. This number is reasonable because the agent should be able to solve the Lunar Lander environment in less than 2000 episodes using this notebook’s default parameters.
  • Line 5: We use the .reset() method to reset the environment to the initial state and get the initial state.
  • Line 6: We start the inner loop. Notice that we have set 𝑇=T= max_num_timesteps = 1000. This means that the episode will automatically terminate if the episode hasn’t terminated after 1000 time steps.
  • Line 7: The agent observes the current state and chooses an action using an πœ–Ο΅-greedy policy. Our agent starts out using a value of πœ–=Ο΅= epsilon = 1 which yields an πœ–Ο΅-greedy policy that is equivalent to the equiprobable random policy. This means that at the beginning of our training, the agent is just going to take random actions regardless of the observed state. As training progresses we will decrease the value of πœ–Ο΅ slowly towards a minimum value using a given πœ–Ο΅-decay rate. We want this minimum value to be close to zero because a value of πœ–=0Ο΅=0 will yield an πœ–Ο΅-greedy policy that is equivalent to the greedy policy. This means that towards the end of training, the agent will lean towards selecting the action that it believes (based on its past experiences) will maximize 𝑄(𝑠,π‘Ž)Q(s,a). We will set the minimum πœ–Ο΅ value to be 0.01 and not exactly 0 because we always want to keep a little bit of exploration during training. If you want to know how this is implemented in code we encourage you to take a look at the utils.get_action function in the utils module.
  • Line 8: We use the .step() method to take the given action in the environment and get the reward and the next_state.
  • Line 9: We store the experience(state, action, reward, next_state, done) tuple in our memory_buffer. Notice that we also store the done variable so that we can keep track of when an episode terminates. This allowed us to set the 𝑦y targets in Exercise 2.
  • Line 10: We check if the conditions are met to perform a learning update. We do this by using our custom utils.check_update_conditions function. This function checks if 𝐢=C= NUM_STEPS_FOR_UPDATE = 4 time steps have occured and if our memory_buffer has enough experience tuples to fill a mini-batch. For example, if the mini-batch size is 64, then our memory_buffer should have more than 64 experience tuples in order to pass the latter condition. If the conditions are met, then the utils.check_update_conditions function will return a value of True, otherwise it will return a value of False.
  • Lines 11 - 14: If the update variable is True then we perform a learning update. The learning update consists of sampling a random mini-batch of experience tuples from our memory_buffer, setting the 𝑦y targets, performing gradient descent, and updating the weights of the networks. We will use the agent_learn function we defined in Section 8 to perform the latter 3.

  • Line 15: At the end of each iteration of the inner loop we set next_state as our new state so that the loop can start again from this new state. In addition, we check if the episode has reached a terminal state (i.e we check if done = True). If a terminal state has been reached, then we break out of the inner loop.

  • Line 16: At the end of each iteration of the outer loop we update the value of πœ–Ο΅, and check if the environment has been solved. We consider that the environment has been solved if the agent receives an average of 200 points in the last 100 episodes. If the environment has not been solved we continue the outer loop and start a new episode.

Finally, we wanted to note that we have included some extra variables to keep track of the total number of points the agent received in each episode. This will help us determine if the agent has solved the environment and it will also allow us to see how our agent performed during training. We also use the time module to measure how long the training takes.

start = time.time()

num_episodes = 2000
max_num_timesteps = 1000

total_point_history = []

num_p_av = 100    # number of total points to use for averaging
epsilon = 1.0     # initial Ξ΅ value for Ξ΅-greedy policy

# Create a memory buffer D with capacity N
memory_buffer = deque(maxlen=MEMORY_SIZE)

# Set the target network weights equal to the Q-Network weights
target_q_network.set_weights(q_network.get_weights())

for i in range(num_episodes):
    
    # Reset the environment to the initial state and get the initial state
    state = env.reset()
    total_points = 0
    
    for t in range(max_num_timesteps):
        
        # From the current state S choose an action A using an Ξ΅-greedy policy
        state_qn = np.expand_dims(state, axis=0)  # state needs to be the right shape for the q_network
        q_values = q_network(state_qn)
        action = utils.get_action(q_values, epsilon)
        
        # Take action A and receive reward R and the next state S'
        next_state, reward, done, _ = env.step(action)
        
        # Store experience tuple (S,A,R,S') in the memory buffer.
        # We store the done variable as well for convenience.
        memory_buffer.append(experience(state, action, reward, next_state, done))
        
        # Only update the network every NUM_STEPS_FOR_UPDATE time steps.
        update = utils.check_update_conditions(t, NUM_STEPS_FOR_UPDATE, memory_buffer)
        
        if update:
            # Sample random mini-batch of experience tuples (S,A,R,S') from D
            experiences = utils.get_experiences(memory_buffer)
            
            # Set the y targets, perform a gradient descent step,
            # and update the network weights.
            agent_learn(experiences, GAMMA)
        
        state = next_state.copy()
        total_points += reward
        
        if done:
            break
            
    total_point_history.append(total_points)
    av_latest_points = np.mean(total_point_history[-num_p_av:])
    
    # Update the Ξ΅ value
    epsilon = utils.get_new_eps(epsilon)

    print(f"\rEpisode {i+1} | Total point average of the last {num_p_av} episodes: {av_latest_points:.2f}", end="")

    if (i+1) % num_p_av == 0:
        print(f"\rEpisode {i+1} | Total point average of the last {num_p_av} episodes: {av_latest_points:.2f}")

    # We will consider that the environment is solved if we get an
    # average of 200 points in the last 100 episodes.
    if av_latest_points >= 200.0:
        print(f"\n\nEnvironment solved in {i+1} episodes!")
        q_network.save('lunar_lander_model.h5')
        break
        
tot_time = time.time() - start

print(f"\nTotal Runtime: {tot_time:.2f} s ({(tot_time/60):.2f} min)")

We can plot the total point history along with the moving average to see how our agent improved during training. If you want to know about the different plotting options available in the utils.plot_history function we encourage you to take a look at the utils module.

# Plot the total point history along with the moving average
utils.plot_history(total_point_history)

Trained Agent in Action

Now that we have trained our agent, we can see it in action. We will use the utils.create_video function to create a video of our agent interacting with the environment using the trained π‘„Q-Network. The utils.create_video function uses the imageio library to create the video. This library produces some warnings that can be distracting, so, to suppress these warnings we run the code below.

# Suppress warnings from imageio
import logging
logging.getLogger().setLevel(logging.ERROR)

Create Video

In the cell below we create a video of our agent interacting with the Lunar Lander environment using the trained q_network. The video is saved to the videos folder with the given filename. We use the utils.embed_mp4 function to embed the video in the Jupyter Notebook so that we can see it here directly without having to download it.

We should note that since the lunar lander starts with a random initial force applied to its center of mass, every time you run the cell below you will see a different video. If the agent was trained properly, it should be able to land the lunar lander in the landing pad every time, regardless of the initial force applied to its center of mass.

filename = "./videos/lunar_lander.mp4"

utils.create_video(filename, env, q_network)
utils.embed_mp4(filename)