def my_dense(a_in, W, b, g):
"""
Computes dense layer
Args:
a_in (ndarray (n, )) : Data, 1 example
W (ndarray (n,j)) : Weight matrix, n features per unit, j units
b (ndarray (j, )) : bias vector, j units
g activation function (e.g. sigmoid, relu..)
Returns
a_out (ndarray (j,)) : j units
"""
units = W.shape[1]
a_out = np.zeros(units)
for j in range(units):
w = W[:,j]
z = np.dot(w, a_in) + b[j]
a_out[j] = g(z)
return(a_out)NN in Numpy - Digit Recognition II
This is a continuation of Didit Recognintion I. Use all steps in that page up to now
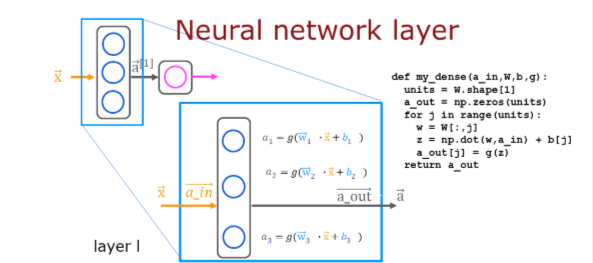
Build Layer
Below, build a dense layer subroutine. The example in lecture utilized a for loop to visit each unit (j) in the layer and perform the dot product of the weights for that unit (W[:,j]) and sum the bias for the unit (b[j]) to form z. An activation function g(z) is then applied to that result. This section will not utilize some of the matrix operations described in the optional lectures. These will be explored in a later section.
.
Check
# Quick Check
x_tst = 0.1*np.arange(1,3,1).reshape(2,) # (1 examples, 2 features)
W_tst = 0.1*np.arange(1,7,1).reshape(2,3) # (2 input features, 3 output features)
b_tst = 0.1*np.arange(1,4,1).reshape(3,) # (3 features)
A_tst = my_dense(x_tst, W_tst, b_tst, sigmoid)
print(A_tst)
Build Layers
# build 3 layer NN using my_dense function
def my_sequential(x, W1, b1, W2, b2, W3, b3):
a1 = my_dense(x, W1, b1, sigmoid)
a2 = my_dense(a1, W2, b2, sigmoid)
a3 = my_dense(a2, W3, b3, sigmoid)
return(a3)Copy Weights
Copy weights from our example using TF
W1_tmp,b1_tmp = layer1.get_weights()
W2_tmp,b2_tmp = layer2.get_weights()
W3_tmp,b3_tmp = layer3.get_weights()Predict
# make predictions
prediction = my_sequential(X[0], W1_tmp, b1_tmp, W2_tmp, b2_tmp, W3_tmp, b3_tmp )
if prediction >= 0.5:
yhat = 1
else:
yhat = 0
print( "yhat = ", yhat, " label= ", y[0,0])
prediction = my_sequential(X[500], W1_tmp, b1_tmp, W2_tmp, b2_tmp, W3_tmp, b3_tmp )
if prediction >= 0.5:
yhat = 1
else:
yhat = 0
print( "yhat = ", yhat, " label= ", y[500,0])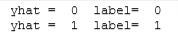
TF vs Numpy Predictions
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
# You do not need to modify anything in this cell
m, n = X.shape
fig, axes = plt.subplots(8,8, figsize=(8,8))
fig.tight_layout(pad=0.1,rect=[0, 0.03, 1, 0.92]) #[left, bottom, right, top]
for i,ax in enumerate(axes.flat):
# Select random indices
random_index = np.random.randint(m)
# Select rows corresponding to the random indices and
# reshape the image
X_random_reshaped = X[random_index].reshape((20,20)).T
# Display the image
ax.imshow(X_random_reshaped, cmap='gray')
# Predict using the Neural Network implemented in Numpy
my_prediction = my_sequential(X[random_index], W1_tmp, b1_tmp, W2_tmp, b2_tmp, W3_tmp, b3_tmp )
my_yhat = int(my_prediction >= 0.5)
# Predict using the Neural Network implemented in Tensorflow
tf_prediction = model.predict(X[random_index].reshape(1,400))
tf_yhat = int(tf_prediction >= 0.5)
# Display the label above the image
ax.set_title(f"{y[random_index,0]},{tf_yhat},{my_yhat}")
ax.set_axis_off()
fig.suptitle("Label, yhat Tensorflow, yhat Numpy", fontsize=16)
plt.show()
Vectorization
We will use vectorization to speed the calculations. Below we will use an operation that computes output for all units in a layer. X and W must be compatible.
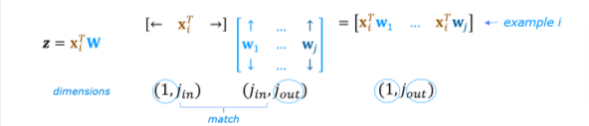
x = X[0].reshape(-1,1) # column vector (400,1)
z1 = np.matmul(x.T,W1) + b1 # (1,400)(400,25) = (1,25)
a1 = sigmoid(z1)
print(a1.shape)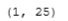
We can go further and compute all examples in one Matrix
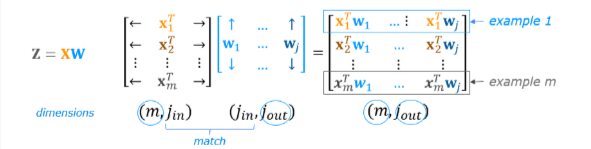
The full operation is 𝐙=𝐗𝐖+𝐛Z=XW+b. This will utilize NumPy broadcasting to expand 𝐛b to 𝑚m rows.
Build Layers
def my_dense_v(A_in, W, b, g):
"""
Computes dense layer
Args:
A_in (ndarray (m,n)) : Data, m examples, n features each
W (ndarray (n,j)) : Weight matrix, n features per unit, j units
b (ndarray (1,j)) : bias vector, j units
g activation function (e.g. sigmoid, relu..)
Returns
A_out (tf.Tensor or ndarray (m,j)) : m examples, j units
"""
Z = np.matmul(A_in,W) + b
A_out = g(Z)
return(A_out)Test
X_tst = 0.1*np.arange(1,9,1).reshape(4,2) # (4 examples, 2 features)
W_tst = 0.1*np.arange(1,7,1).reshape(2,3) # (2 input features, 3 output features)
b_tst = 0.1*np.arange(1,4,1).reshape(1,3) # (1,3 features)
A_tst = my_dense_v(X_tst, W_tst, b_tst, sigmoid)
print(A_tst)
Build NN
def my_sequential_v(X, W1, b1, W2, b2, W3, b3):
A1 = my_dense_v(X, W1, b1, sigmoid)
A2 = my_dense_v(A1, W2, b2, sigmoid)
A3 = my_dense_v(A2, W3, b3, sigmoid)
return(A3)Copy Weights
W1_tmp,b1_tmp = layer1.get_weights()
W2_tmp,b2_tmp = layer2.get_weights()
W3_tmp,b3_tmp = layer3.get_weights()Predict
Let’s make a prediction with all the examples at once
Prediction = my_sequential_v(X, W1_tmp, b1_tmp, W2_tmp, b2_tmp, W3_tmp, b3_tmp )
Prediction.shape
Apply Threshold
# threshold of 0.5
Yhat = (Prediction >= 0.5).astype(int)
print("predict a zero: ",Yhat[0], "predict a one: ", Yhat[500])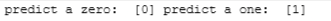
Plot
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
# You do not need to modify anything in this cell
m, n = X.shape
fig, axes = plt.subplots(8, 8, figsize=(8, 8))
fig.tight_layout(pad=0.1, rect=[0, 0.03, 1, 0.92]) #[left, bottom, right, top]
for i, ax in enumerate(axes.flat):
# Select random indices
random_index = np.random.randint(m)
# Select rows corresponding to the random indices and
# reshape the image
X_random_reshaped = X[random_index].reshape((20, 20)).T
# Display the image
ax.imshow(X_random_reshaped, cmap='gray')
# Display the label above the image
ax.set_title(f"{y[random_index,0]}, {Yhat[random_index, 0]}")
ax.set_axis_off()
fig.suptitle("Label, Yhat", fontsize=16)
plt.show()
Misclassified
fig = plt.figure(figsize=(1, 1))
errors = np.where(y != Yhat)
random_index = errors[0][0]
X_random_reshaped = X[random_index].reshape((20, 20)).T
plt.imshow(X_random_reshaped, cmap='gray')
plt.title(f"{y[random_index,0]}, {Yhat[random_index, 0]}")
plt.axis('off')
plt.show()