NN Training with TF
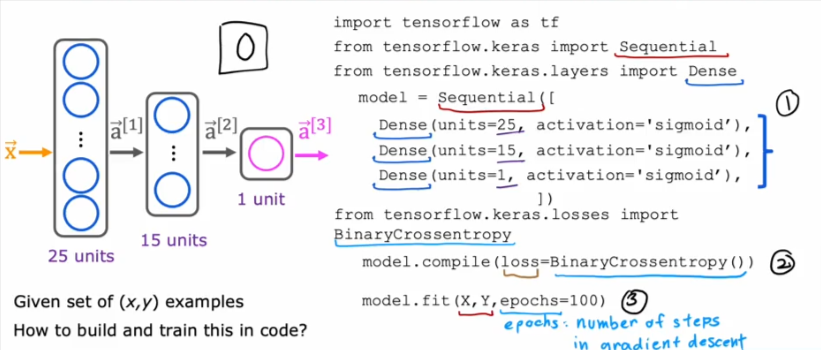
We’ve covered the digit recognition model, and we’ll go into details here on how to train it with TF. Here is a recap and an overview of what we’ve done and will do
- Remember we have a 3 layer model with
- 25, 15 & 1 unit per layer
- Given (x,y) as examples (input)
- 1- We sequentially string together 3 layers using the Sequential() function
- 2-Ask TF to compile the model using a Loss and Gradient Descent procedures, in this case we will use BinaryCrossentropy()
- Binay is because we want to classify if the value is a 0 or 1
- Of course if you were wanting a regression model then you can use a different function to calculate the Loss and GD
- 3- Call the fit() to train the model using X and Y as inputs as well as
- Set the number of iterations with epochs
Train NN

Logistic Regression
So let’s break it down. Let’s go back to how we trained a logistic regression model.
- Specify how to compute the output given input x and parameters w, b and therefore we specified the model fw,b(x)=?
- We then specified the loss and cost functions to use.
- Remember the loss L(fw,b(x),y) is for one example while the cost is the average summation of all the losses for all the rows and all parameters
- Then we minimize the cost J(w,b) of the function by utilizing GD
Neural Network
- Define the layers
- Compile the model and tell it which loss function to use and then average the summation of all the losses to calculate the cost
- Fit the model to try to minimize the cost of the model
So let’ break down the 3 steps individually
Create Model
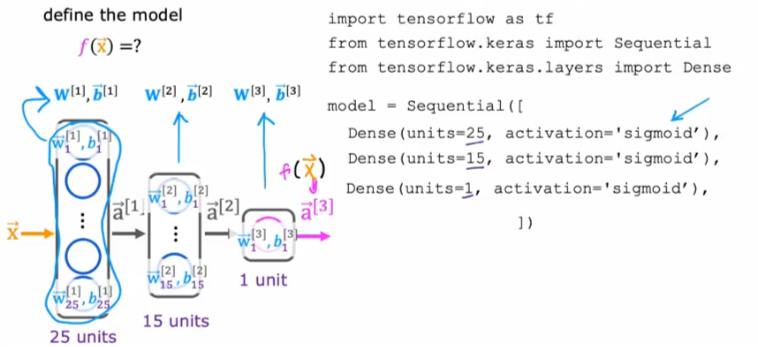
- As shown above we start by defining the model
- We know the parameters for the first layer are w[1], b[1]
- for the second layer: w[2], b[2] and so on
- we identify the number of units per layer
- We are using the logistic regression function sigmoid
- Now we have everything we need to create the model
Loss & Cost Functions

- Since we are working on the handwritten digit classification problem, a binary classification model is what we will need where we are comparing prediction vs target
- In TF the binary logistic loss function is known as Binarycrossentropy
- Keras is a library that contains the Binaycrossentropy function
- So we compile our model using that function to calculate the Loss and Cost of our model
- Having specified the loss for one training example, TF knows that it needs to optimize the cost function for this model while training it on the sample input (training data)
- Remember that the cost function J(W,B) includes the loss for all the parameters for all rows and layers
- Remember that fw,b(x) is the value for each function for each parameter applied to each X or row of training data
- If we were solving a regression problem where we are predicting a number and not categories/classes, we can use a different loss/cost function
- We can use for example the MeanSquaredError() function instead of the BinaryCrossentropy() function
Gradient Descent
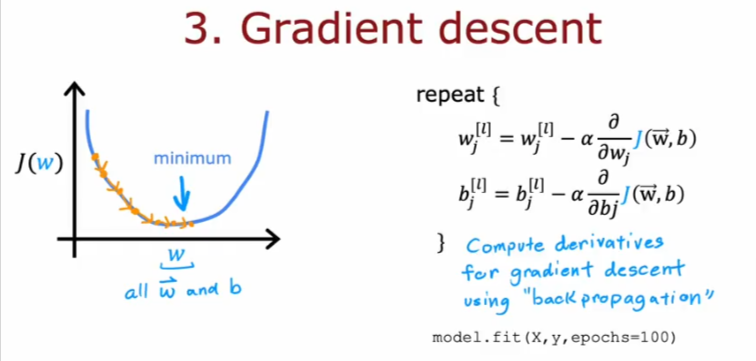
- Finally we will minimize the cost of the model for every parameter using GD
- We set the iteration number
- TF uses back propagation to calculate all the partial derivatives for all the parameters and input rows in the model.fit()
- the fit function requires the input and label, as well as the number of iterations = epochs
- The fit function basically updates the NN parameters in order to reduce the cost