Softmax

Normally you want to substitute your last layer activation function to Softmax if you have a multiclass classification problem.

  • Let’s say we have a 10 classes problem to solve
  • We use ReLU for the first two hidden layers and now we want to use Softmax for the output layer
  • So we calculate z1 - z10 using the output of the previous layer a[2] using the same formulas as we did in the past
  • Then we calculate a1 - a10 for each class using the z values passed to us from the previous layer (this is our estimate of the chance that the value is close to 1) P(y=1|x) for each class
  • Note: the value of Softmax is dependent on each value of zi , in other words each value from z1 to z10 is incorporated into the formula to calculate the output. This is different from other activation functions which are dependent on their own z value (in other words a1 only uses z1 and no other z value)

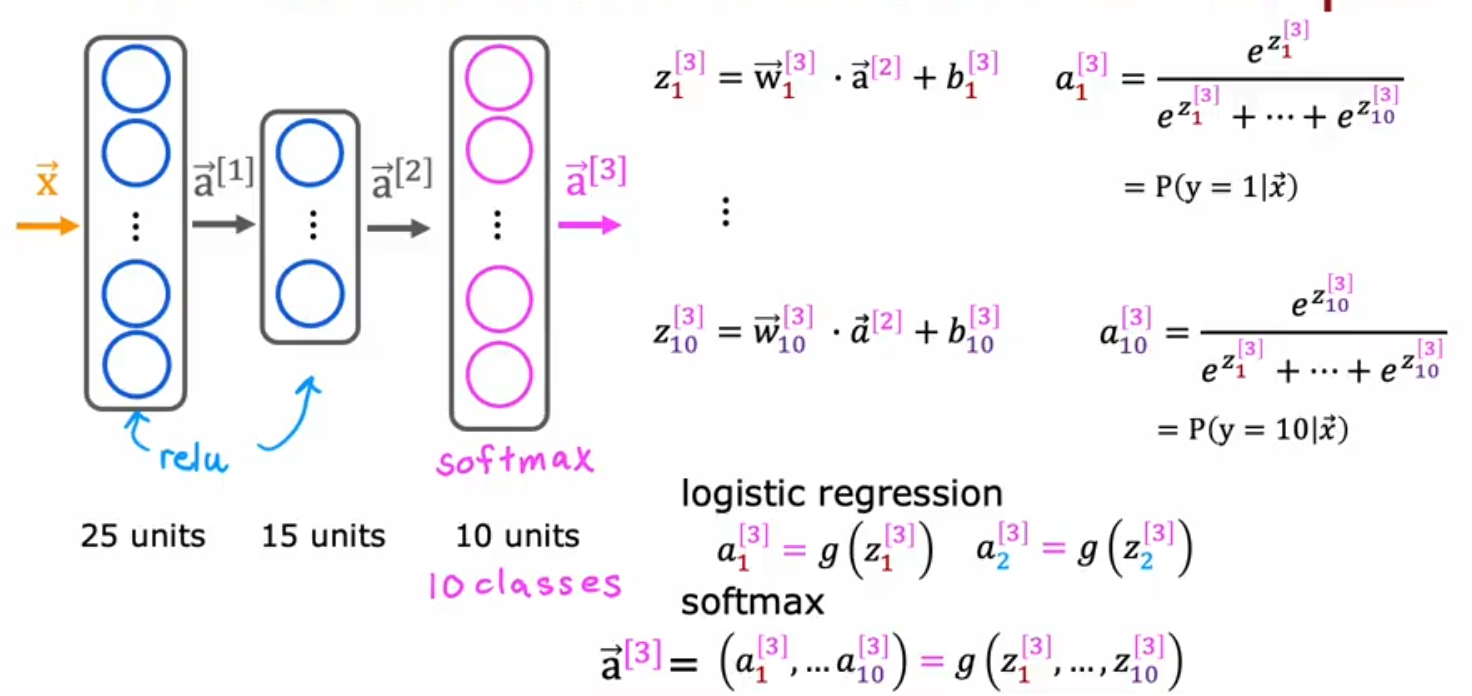
So how do we implement it in TF. We will modify the code in a minute, but here below is the overview

Note:

The major difference is the new dedicated Loss & Cost function used SparseCategoricalCrossentropy function (sparse: for choosing one of the categories and not more)

Improved Loss Functions

In order to be more precise calculating the loss functions we will use this formula. It is basically the same as above with a slight variation as to how we divide by a large number.

Logistic Regression

So substitute with: model.compile(loss=BinaryCrossEntropy(from_logits=True))

Softmax

Substitute with: model.compile(loss=SparseCategoricalCrossEntropy(from_logits=True)) and substitute the last activation function with a linear one

NOTE:

  • Now that we’ve changed the final layer to a linear function it will no longer output a1 .. a10
  • It will output z1 .. z10
  • So we have to convert it as an additional step
  • map it through the logistic function to get z converted to a

Code - Softmax

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from IPython.display import display, Markdown, Latex
from sklearn.datasets import make_blobs
%matplotlib widget
from matplotlib.widgets import Slider
from lab_utils_common import dlc
from lab_utils_softmax import plt_softmax
import logging
logging.getLogger("tensorflow").setLevel(logging.ERROR)
tf.autograph.set_verbosity(0)
def my_softmax(z):
    ez = np.exp(z)              #element-wise exponenial
    sm = ez/np.sum(ez)
    return(sm)

.

TF Method

Create Dataset

# make  dataset for example
centers = [[-5, 2], [-2, -2], [1, 2], [5, -2]]
X_train, y_train = make_blobs(n_samples=2000, centers=centers, cluster_std=1.0,random_state=30)

Softmax Final Activation

  • So here we will use softmax as the final activation function and look at the results
  • Then we will use the more accurate method and compare
  • The model below is implemented with the softmax as an activation in the final Dense layer.
  • The loss function is separately specified in the compile directive.
  • The loss function is SparseCategoricalCrossentropy.
  • In this model, the softmax takes place in the last layer.
  • The loss function takes in the softmax output which is a vector of probabilities.
model = Sequential(
    [ 
        Dense(25, activation = 'relu'),
        Dense(15, activation = 'relu'),
        Dense(4, activation = 'softmax')    # < softmax activation here
    ]
)
model.compile(
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    optimizer=tf.keras.optimizers.Adam(0.001),
)

model.fit(
    X_train,y_train,
    epochs=10
)

Because the softmax is integrated into the output layer, the output is a vector of probabilities.

p_nonpreferred = model.predict(X_train)
print(p_nonpreferred [:2])
print("largest value", np.max(p_nonpreferred), "smallest value", np.min(p_nonpreferred))

Improved & Preferred

preferred_model = Sequential(
    [ 
        Dense(25, activation = 'relu'),
        Dense(15, activation = 'relu'),
        Dense(4, activation = 'linear')   #<-- Note
    ]
)
preferred_model.compile(
    loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),  #<-- Note
    optimizer=tf.keras.optimizers.Adam(0.001),
)

preferred_model.fit(
    X_train,y_train,
    epochs=10
)

Notice that in the preferred model, the outputs are not probabilities, but can range from large negative numbers to large positive numbers. The output must be sent through a softmax when performing a prediction that expects a probability. Let’s look at the preferred model outputs:

p_preferred = preferred_model.predict(X_train)
print(f"two example output vectors:\n {p_preferred[:2]}")
print("largest value", np.max(p_preferred), "smallest value", np.min(p_preferred))

Process Output

sm_preferred = tf.nn.softmax(p_preferred).numpy()
print(f"two example output vectors:\n {sm_preferred[:2]}")
print("largest value", np.max(sm_preferred), "smallest value", np.min(sm_preferred))

Find Most likely Category

for i in range(5):
    print( f"{p_preferred[i]}, category: {np.argmax(p_preferred[i])}")